Check Template Verify is a new opcode for Bitcoin which allows transaction issuers to split up their transaction into send and receive components. See https://utxos.org for more information. This is potentially a big benefit because end users can realize faster confirmations on pending transactions.
There is a concern that CTV would result in higher overall chain utilization (because of overhead) than existing batching solutions. Ignoring the benefits that CTV can have for earlier confirmations, it would be bad to introduce a change to Bitcoin that causes users to be wasteful of chain space.
This simulation proposes and analyzes a model where CTV is a good user of chainspace.
The point of this simulation is to show that CTV is not worse than status quo with respect to scalability. I hacked this together in a couple of hours so feel free to suggest tweaks (via PR or issue) to make it more realistic & there may correct errors of course.
Setup
I am modeling a situation where every block:
- a business sees a number of payment requests per second
- the rest of the world does another number of payments per second
- Each payment and payment request has a priority
- Priorities are drawn randomly from a distribution
Because priority is relative, just the shape of the distribution of priority matters. The default distribution is lognormal, but others are included to check that the result holds across other distributions.
The distribution of priority is the big hypothetical point – what distributions are the actual priorities of outbound payments from businesses? Are they constant – then this model is invalid. But if they fall on a distribution, then carry on reading…
Specific Assumptions
If more than one payment request comes in within a single block period, it may make sense to issue them in the same transaction if they are around the same priority.
If they come in at different priorities, it may make sense to split up transactions into batches based on their priority. If I have a batch that contains payment A and priority A.p, and B and B.p, then the entire batch should be at priority max(A.p, B.p). If A.p and B.p are too far apart, then batching them is inefficient as one has to overpay to achieve the same feerate for the transaction.
Thus, we assume:
- Transactions come in different priorities
- A batch must pay a rate appropriate for the highest priority payment in the batch
Strategies
Consider 4 batching implementations:
Strategy “NOBATCH_MED”:
In this strategy we just issue transactions per payment, no batching or anything else fancy. We pay the median fee of the last block.
Strategy “BATCH_MAX”:
In this strategy we batch transactions all together and then we pay the min of the median or max feerate in batch
Strategy “BATCH_GROUP_MAX”:
In this strategy we batch transactions of similar feerate together and then we pay the min of the median or max feerate in each batch
Strategy “BATCH_GROUP_MAX_CTV”:
In this strategy we batch transactions of similar feerate together and then we pay the min of the median or max feerate in each batch But instead of making independent batches, we put them through one layer of a high fee paying CTV root.
Strategy “BATCH_GROUP_MAX_CTV_MIN_FOLLOWUP”:
In this strategy we batch transactions of similar feerate together and then we pay the min of the min feerate over the last ten blocks or max feerate in each batch But instead of making independent batches, we put them through one layer of a high fee paying CTV root with n_bins outputs.
We cut through bins with only one element
Pay 10-block low (but mineable) fee for each bin
Strategy “BATCH_GROUP_MAX_DOUBLE_CTV_MIN_FOLLOWUP”:
In this strategy we batch transactions of similar feerate together and then we pay the min of the min feerate over the last ten blocks or max feerate in each batch But instead of making independent batches, we put them through two layers of CTV: a high fee paying CTV root with one output, and then a low paying CTV root with n_bins outputs.
We cut through bins with only one element Pay 10-block low (but mineable) fee for each bin and second root
Strategy “BATCH_GROUP_MAX_DOUBLE_CTV_CPFP_FOLLOWUP”:
In this strategy we batch transactions of similar feerate together and then we pay 0 (leaving it up to CPFP) But instead of making independent batches, we put them through two layers of CTV: a high fee paying CTV root with one output, and then a 0 paying CTV root with n_bins outputs.
We cut through bins with only one element
This puts people into priority bins, but allows CPFP to commit to the fees later avoiding over-offering of fees.
Pay 10-block low (but mineable) fee for each bin and second root
Note that the simulations are not doing anything smart for binning, just calling numpy.histogram. There’s probably an optimal solution.
The BATCH_GROUP_MAX_CTV fan-out is also the “obvious” one – pay a CTV for each bin in the txn root, and then each CTV expands to the entire bin, skipping the CTV is there’s only one bin. The other CTV strategies present a couple optimizations which can further improve the efficiency.
Claims
My claims are as follows:
A. If it is lower fee to use priority binned batching than single batching, then users will use priority binned batching for economic fee reducing reasons. B. If CTV priority binned batching is more blockspace efficient that priority binned batching, and hypothesis A. holds, this will overall make the chain usage lower. C. If CTV Priority Binned batching is more fee efficient than binned batching or normal binned batching, it will be preferred. D. If B., then C.. E. If A. and B., then CheckTemplateVerify does not decrease the availability of chain space, even marginally so.
Results
I recommend you run main.py yourself to see for yourself (and zoom around), as well as play around with different parameters. The code is reasonably documented.

And zoomed in on the interesting bits:
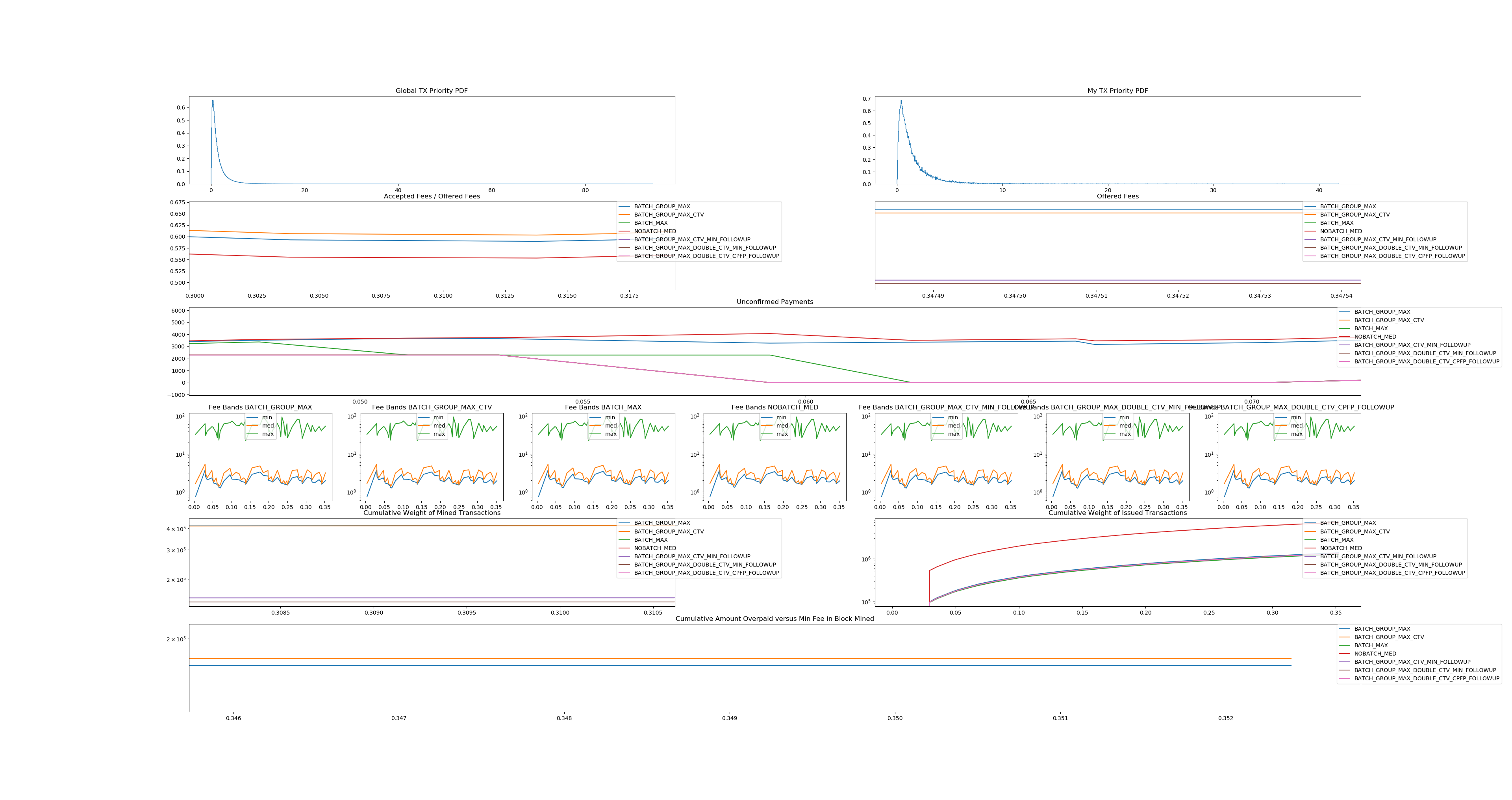
This confirms all of the claims presented previously, and shows that CTV can be a better user of chain space than existing methods.
This is an important point! We’ve demonstrated that CTV is better in terms of chain space but we haven’t discussed the “first order” benefits of CTV for decongesting the mempool. See https://utxos.org/analysis/bip_simulation/. This means not only will CTV help us confirm more payments more quickly, but we’ll also use less space. A pure win-win.
Limitations
A better simulation would allow re-bundling the offered-but-not-taken fees into a new RBF batch, which would benefit Priority Batching but not CTV batching.
The BATCH_GROUP_MAX_DOUBLE_CTV_CPFP_FOLLOWUP strategy also does not actually use CPFP, a better simulation would measure how much fee savings can be realized with CPFP.
If the assumptions around priority distributions do not hold, then CTV still has benefits worth pursuing, but we should more carefully think about the space usage impact on Bitcoin. With the strategies for batching presented, the overall chain usage is a constant amount more, so the impact is at least non-asymptotic. However, if CTV is still used in a tree structure to minimize individual redeemer overhead, then what is the overhead? Assuming a radix of r, we need N/r base layer transactions. And then N/r^2 above that, etc. For r >= 1, 1/r^0 + 1/r^1…1/r^inf = 1/(1-1/r). So CTV would use about 10% more transactions for a radix of 10, 5% more for a radix of 20, 1% for a radix of 100. The transactions roughly corresponds to the amount of space used as well. Overall, this means that businesses can balance out the worth of per-user decongesting effects (which are optimal around radix 4) with fee savings on a dynamic basis, and able to dial down the overhead to very little.

